English
Zobacz więcej:
- dla uczniów szkół podstawowych: oij.edu.pl/start/
- dla uczniów szkół średnich: oi.edu.pl/l/jak_zaczac/
Zadanie Odcinki (odc)
Segments
Memory limit: 32 MB
Lets consider a set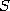 
of 
vertical segments on the plain (segments include their end points).
None of the elements of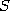 
have a point in common.
Two segments are said to "see each other" if there exists a horizontal segment, which connects
them and does not have any common points with other segments from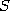 
.
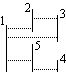
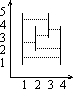
On the figure below, there is an example set of segments. Pairs of segments that can see each other, are: 1-2, 1-3, 2-3, 1-5 and 4-5. The segments 1 and 4 do not see each other.
For a given number 
, we search for a set 
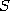of 
vertical segments such that the number of pairs of segments which can see each other is as big as possible.
Task
Write a program which:
- reads the number
from the standard input,
- computes locations of
vertical segments, such that
- none of them have a point in common,
- the number of pairs of segments which can see each other is as big as possible,
- writes the answer to the standard output.
Input
The first and only line of the standard input contains one integer 
(
).
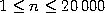Output
The first line of the standard output should contain one integer - maximal number of pairs of segments that can see each other.
Each of the following 
lines should identify the coordinates of one segment.
Line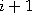 
(for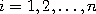 
) consists of three integers:
, 
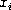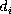i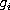 
(
,
),
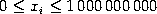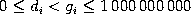separated by a single space. They represent the segment which connects the points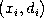 
and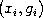 
.
If there are more than one correct arrangement of 
segments, your program can write out any of them.
Example
For the input data:
4
the correct result is:
6 1 1 5 2 2 4 3 3 5 4 1 4
Task author: Jakub Radoszewski.